プラレール線型代数 (1)

この記事は夏合宿における @akamah の成果をだいぶ寒くなった頃にまとめたものです．

概要

本記事では，プラレールを線型代数的な視点から眺めることによって， レイアウトの理解，特に曲線レールに対する解釈を試みます．

レール

プラレールには様々なレールがありますが，ここでは直線レールと曲線レールについてのみ考えます． 直線レールの長さを1とすると，曲線レールは半径が長さ1の円周の8分の1の円弧です．

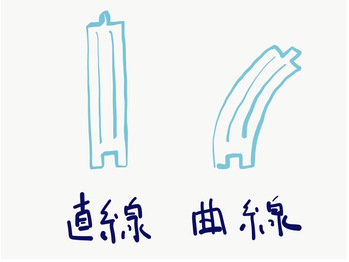
ベクトル

線型代数的な解釈ということで，“レールの持つベクトル”というものを考えてみます． これはレールの片方を原点として，もう片方へ向かうベクトルとします．

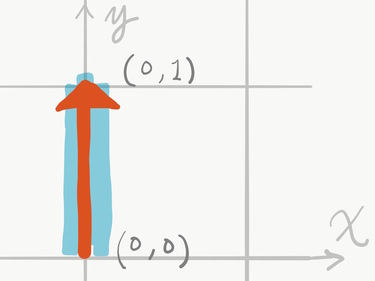
ベクトルの合成

さっそくベクトルの合成を考えます． レールの持つベクトルを合成するときは，実際のレールに必要な「ちゃんと向きが合っている」という条件を無視することにします． すなわち，位置さえ正確に合っていればレールをつないで伸ばせる，と都合よく考えます．

この仮定はレールをベクトルとして考えるためのやや人為的なもので， 例えば以下のような連結もベクトルとして考える場合はちょっと許してしまおうということです ¹．

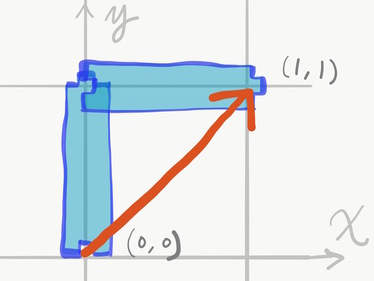
曲線レールのベクトル

さてさて，曲線レールのベクトルも描いてみましょう．すると不思議なこと（？）が起こります．

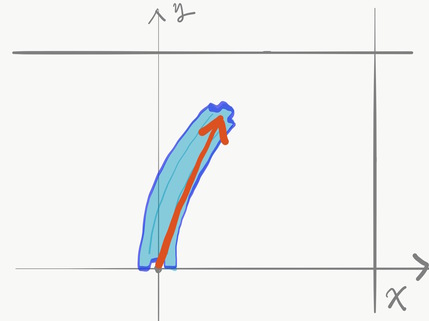
原点から伸びた先の点はどういった座標になるでしょうか？計算してみます．

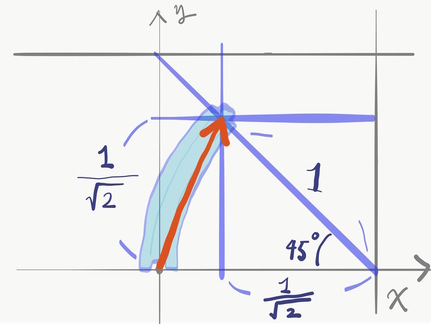
上図のように補助線を引けば，矢印の先端の座標がわかります．

\[(x, y) = (1 - 1 / \sqrt{2}, 1 / \sqrt{2})\]

平方根が出てきました．でも平方根ってちょっとめんどくさいですね． もうすこし分かりやすく曲線レールの持つベクトルを表せないでしょうか．

曲線を直線で表す

ところで，単位円の中心からの距離は等しく1であり，曲線レールは8分の1の円弧です． そこで，端っこを無理やりくっつけることで， 次のように2つの直線の連結だと捉えることもできます．

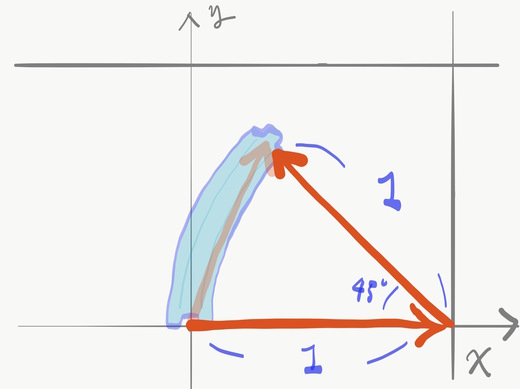
すると，曲線レールのベクトルは，タテまたはヨコ方向とななめ方向の長さ1のベクトルを連結したものと言えます． すなわち，ベクトルとして考えることによって曲線レールを直線2つだと捉えることができるようになりました．

レールのベクトル表現

すると直線レールおよび曲線レールのベクトルをまとめて表す方法がひとつ思いつきます． タテヨコななめ方向のベクトルを整数倍して足し合わせてベクトル空間のようなものを作る方法です (注 ²)．

まず，\(\boldsymbol{x}\) と \(\boldsymbol{y}\)を(x, y)平面の標準基底とします． そして，以下のように新しい基底ベクトルを取ります．

\[\begin{align} \boldsymbol{a} &= \boldsymbol{x} \\ \boldsymbol{b} &= \frac{\boldsymbol{x} + \boldsymbol{y}}{\sqrt{2}} \\ \boldsymbol{c} &= \boldsymbol{y} \\ \boldsymbol{b} &= \frac{-\boldsymbol{x} + \boldsymbol{y}}{\sqrt{2}} \\ \end{align}\]

そしてこれらの4つの基底ベクトルの整数線型結合（整数倍して足し合わせる）でレール上の座標系を表します．

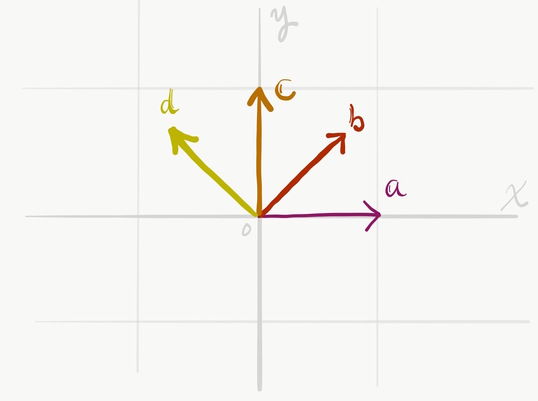
つまり，(x, y) 座標ではなく，この (a, b, c, d) 座標でレールのベクトルを表そうというアイディアです．

例を挙げると，横に伸びる直線レールのベクトルはx軸方向に長さ1のレールなので， \((a, b, c, d) = (1, 0, 0, 0)\) となり，(x, y)座標とあまり変わらないですが，斜めの成分が無いことが明示されます．

また，原点から左下に向かって直線レールを2つつないだ時のベクトルは \((a, b, c, d) = (0, -2, 0, 0)\) と表されます．これは右上方向の基底ベクトル \(\boldsymbol{b}\) にマイナスをつけて逆向きにしてから，長さの2倍をかけたベクトルとなります．

以後，(a, b, c, d)座標のベクトルは単に数字を4つ並べて書くものとします

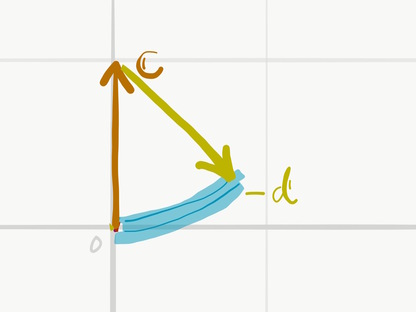
問題の曲線レールですが，原点から下図のように置いた曲線レールのベクトルは \((0, 0, 1, -1)\) となります． これは，上方向に長さ1，右下（つまり，左上の逆）方向に長さ1の成分を持ったベクトル（つまり \(\boldsymbol{c} - \boldsymbol{d}\) ）です．

れいの法則

ベクトル表現を用いて れいの法則 ³と呼ばれる法則を確認してみようと思います． れいの法則とは，以下の2通りのレールが同じ地点にたどり着くという法則です． （画像は三谷先生の鉄道模型コースシミュレータにて作成しました）

まず左側から確認します．6本のレールのベクトルを下から順に足し合わせると，こうなります．

\[\begin{align} & (0, 0, 1, 0) + (0, 0, 1, 0) + (1, 0, 0, 1) + (0, 0, 1, -1) + (0, 1, -1, 0) + (0, 1, -1, 0) \\ = \ & (1, 2, 1, 0) \end{align}\]

続いて右側はこうなります．

\[\begin{align} & (1, 0, 0, 1) + (0, 1, 0, 0) + (0, 1, 0, 0) + (0, 0, 1, -1) \\ = \ & (1, 2, 1, 0) \end{align}\]

2つのレールのベクトルが一致しました．やったね！

この計算では律儀にすべてのレールのベクトルを足して計算していましたが， 現実のよく扱うレイアウトではななめ方向はそこまで多く出てこなく（たぶん）， 縦横方向はわりと合わせやすいため， ななめ方向の成分だけをカウントすることにすれば暗算も簡単です．

このように，ベクトル表現を使わずにきっちり計算していたならば， \(1 / \sqrt{2}\)がたくさん出てきて大変になっていたところを， 曲線レールはななめ方向の成分を持つ， という風にベクトル表現で考えるとちょっと楽になることがあります．

まとめ

この記事では，プラレールのレールをベクトルとして考え， さらに斜めの直線成分をとらえることで， 曲線レールを扱いやすいベクトルの表現を紹介しました．

プラレールのベクトル表現に関しては面白い応用がいくつかあります．

続きはその時に．

---

1. 補足しますと，三谷先生の結果 より，レールのはじっこの位置を変えずに向きを変えることはできるため，方向についてはひとまず考えなくてもよいことになります． ↩

2. 整数は体ではないので，厳密にはベクトル空間とは言えませんので，ベクトル空間のようなものと言い表しました．2次元平面に基底が4つあるのは係数が整数であるゆえです． ↩

3. 原典が見当たりませんでしたが，こちらの議論を参考にしました（アクセス：2017/11/03）： プラレールの組み合わせの法則議論 ↩